Электротехника. Основы. Закон Ома
В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.
Закон Ома
Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.
Закон Ома для участка цепи без ЭДС
Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:
\begin{equation} I = {U_{ab}\over R}; \end{equation}Где:
- I - ток через участок ab электрической цепи;
- Uab - напряжение на участке ab электрической цепи;
- R - сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = U_{ab} × G; \end{equation}Где:
- G - проводимость участка ab электрической цепи.
Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.
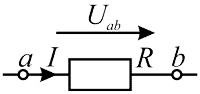
Рисунок 1 - Участок цепи без ЭДС
Закон Ома для участка цепи содержащего ЭДС
Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {U_{ab} + E\over R}; \end{equation}Где:
- I - ток через участок ac электрической цепи;
- Uab - напряжение на участке ab электрической цепи;
- E - ЭДС на участке bс электрической цепи;
- R - сопротивление участка ab электрической цепи.
Или через проводимость:
\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}Где:
- G - проводимость участка ab электрической цепи.
Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.
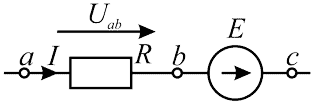
Рисунок 2 - Участок цепи содержащий ЭДС
Закон Ома для полной цепи
Закон формулируется следующим образом [1, стр.34][2, стр.17]:
\begin{equation} I = {E\over {R + r}}; \end{equation}Где:
- I - ток в электрической цепи;
- E - ЭДС электрической цепи;
- R - сопротивление электрической цепи;
- r - внутреннее сопротивление источника ЭДС.
Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).
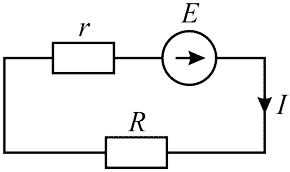
Рисунок 3 - Полная цепь
На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на Rп
\begin{equation} I = {E\over R_п}; \end{equation}Где:
- Rп - полное сопротивление электрической цепи (включая сопротивление источника ЭДС).
Закон Ома в дифференциальной форме
Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].
\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}Где:
- \(\vec\jmath\) - плотность тока;
- ρ - удельное сопротивление;
- \(\vec E\) - напряжённость электрического поля.
Примеры применения
Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.
Пример 1
Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.
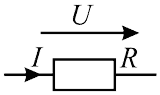
Рисунок 4 - Схема к 1 и 2-му примеру
Для решения задания воспользуемся выражением (1):
\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}Пример 2
Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.
Для решения задания преобразуем выражение (2) относительно G:
\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}Пример 3
Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.
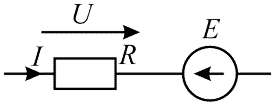
Рисунок 5 - Схема к 3-му примеру
Для решения задания преобразуем выражение (3) относительно E:
\begin{equation} I = {U - E\over R} \ \Rightarrow \ {I × R} = {U - E} \ \Rightarrow \ E = {U - I × R}; \end{equation}Подставим в выражение (10) известные величины:
\begin{equation} E = {U - I × R} = {220 - 0,5 × 140} = {150 \ В;} \end{equation}
Пример 4
Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь - 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.
Преобразуем выражение (5) относительно r:
\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E - I × R} \ \Rightarrow \ r = {E - I × R\over I}; \end{equation}Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:
\begin{equation} r = {E - I × R\over I} = {9 - 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}
Использованные термины
Электрический потенциал точки:
Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.
Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.
Электрическое напряжение:
Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: Uab = φa - φb.
Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение - скалярная величина, но на электрических схемах указывают его положительное направление.
Электродвижущая сила (ЭДС):
Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.
ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС - скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.
Электрическое ток:
Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление - направленное движение заряженных частиц.
Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].
Плотность тока:
Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.
Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м2). Плотность тока - векторная величина [4].
Электрическое сопротивление:
Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.
Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление - скалярная величина.
Электрическая проводимость:
Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.
Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость - скалярная величина.
Удельное сопротивление:
Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м2.
Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].
В дальнейшем при использовании вышеперечисленных терминов слово "электрический" будет упускаться.
Список использованных источников
- Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов - Москва: Высшая школа, 1996. - 623 с.
- Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. - 318 с.
- Википедия - Удельное электрическое сопротивление [электронный ресурс] - Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
- Википедия - Плотность тока [электронный ресурс] - Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока
- Автор: Электрик
- Опубликовано:
- Просмотров: 2.5k
