Всё об энергетике

При изученнии работы трансформаторов лучше начинать с упрощеной модели - идеального трансформатора. Такой подход позволяет сосредоточится на сущности процессов протекающих внутри устройства.

Перед чтением этой стать рекомендуем ознакомится с устройством трансформатора.

Допущения идеального трансформатора

Основные допущения принимаемые для идеального трансформатора перечислены ниже [1, c. 118].

• Отсутствуют тепловые потери в обмотках;
• Отсутствуют потери на перемагничевание магнитопровода;
• Весь магнитный поток замыкается по магнитопроводу;
• Магнитный поток сцепляется со всеми витками первичной и вторичной обмотке одинаково;
• Вебер-амперная характеристика магнитопровода линейна.

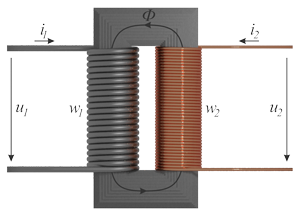
Далее в качестве примера использум схему однофазного двухобмоточного трансформатора, приведенную на рисунке 1.

На рисунке выше изображен общий магнитопровод на котором намотаны первичная обмотка с числом витков \(w_1\) и вторичная обмотка с числом витков \(w_2\). В первичной обмотке протекает ток \(\dot{\imath}_1\), во вторичной - \(\dot{\imath}_2\).

При подключении к первичной обмотке источника переменной ЭДС \(\dot{e}_1\) напряжением \(\dot{u}_1\) в ней возникает переменный ток \(\dot{\imath}_1\). Он, в свою очередь, создает переменный магнитный поток \(\dot{Ф}\) который замыкается по магнитопроводу. Этот магнитный поток создает в первичной обмотке трансформатора переменную ЭДС самоиндукции \(\dot{e}_{L1}\), а во вторичной обмотке - ЭДС \(\dot{e}_{M2}\). Под действием ЭДС \(\dot{e}_{M2}\) во вторичной обмотке возникает переменный ток \(\dot{\imath}_2\), а на её концах появляется напряжение \(\dot{u}_2\). ЭДС \(\dot{e}_{M2}\) и \(\dot{e}_{L1}\) пропорциональны числу витков \(w_2\) и \(w_1\) и скорости изменения магнитного потока \(dФ/dt\). Закон и формула, связывающая эти величины воедино была открыта Максвелом:

\begin{equation} e_1 = -w_1 × {dФ\over dt} \end{equation} \begin{equation} e_2 = -w_2 × {dФ\over dt} \end{equation}

Коэффициент трансформации

Из формул выше видно, что изменяя число витков одной из обмоток мы изменяем ЭДС в ней. Разделив левую и правую части выражений (1) и (2) друг на друга получим коэффициент трансформации:

\begin{equation} {\dot{e}_1\over \dot{e}_2} = {w_1\over w_2} = n \end{equation}

Так как ранее был принят ряд допущений, можно записать: \(\dot{u}_1 = \dot{e}_1,\ \dot{u}_2 = \dot{e}_2\). Тогда коэффициент трансформации будет определятся следующим выражением:

\begin{equation} {\dot{u}_1\over \dot{u}_2} = {w_1\over w_2} = n \end{equation}

Значение \(n\) характеризует отношение напряжений и токов первичной и вторичной обмоток, а также трансформацию сопротивления нагрузки на вторичной обмотке трансформатора.

Отношение токов первичной и вторичной обмотки

Преобразуя формулу (4) для напряжений \(U_1\) и \(U_2\) можно записать:

\begin{equation} {U_1} = {n×U_2} \end{equation}

Заменив в формуле (5) напряжение \(U_1\) и \(U_2\) на выражения \(P_1\over I_1\) и \(P_2\over I_2\) соответственно:

\begin{equation} {P_1\over I_1} = n×{P_2\over I_2} \end{equation}

Из принятых допущений следует, что \(P_1 = P_2 = P\). Разделим выражение (6) на \(P\):

\begin{equation} {1\over I_1} = {n\over I_2} \end{equation}

Умножим выражение (7) на \(I_1×I_2\) чтобы избавится от дроби:

\begin{equation} I_2 = n×I_1 \end{equation}

Выражение (8) отражает отношение токов первичной и вторичной обмоток идеального двухобмоточного трансформатора.

Трансформация сопротивления нагрузки

Для определения зависимости трансформации сопротивления нагрузки рассмотрим мощность, потребляемую нагрузкой \(R_2\):

\begin{equation} P_2 = {I_2}^2×R_2 \end{equation}

Помня, что \(P_1 = P_2\), можно записать следующее:

\begin{equation} {I_1}^2×R_1 = {I_2}^2×R_2 \end{equation}

где \(R_1\) - сопротивление нагрузки подключенной ко вторичной обмотке, приведённое к ВН. Подставляя выражение (8) в выражение (10) получим:

\begin{equation} {{I_2}^2\over n}×R_1 = {I_2}^2×R_2 \end{equation}

Разделив выражение (11) на \({I_2}^2\) и умножив его на \(n^2\) получим формулу приведения сопротивления вторичной обмотки (нагрузки) к первичной.

\begin{equation} R_1 = n^2×R_2 \end{equation}

Обобщая выражения (4) и (8) относительно \(n\) можно записать:

\begin{equation} {U_1\over U_2} = {I_2\over I_1} = {w_1\over w_2} = n \end{equation}

Иначе говоря, трансформатор, при повышении величины напряжения на выводах одной из обмоток (ВН или НН) понижает величину тока в ней, и наооборот при понижении напряжения на выводах одной из обмоток возрастает протекающий по ней ток.

Взаимодействие напряжения, тока, магнитного потока и ЭДС в трансформаторе

Как было написано выше, ЭДС напряжением \(\dot{u}_1\), создает ток \(\dot{\imath}_1\), который в свою очередь создает магнитный поток \(\dot{Ф}\) в магнитопроводе. Этот магнитный поток \(\dot{Ф}\) наводит в первичный обмотке ЭДС самоиндукции \(\dot{e}_1\), а во вторичной ЭДС взаимоиндукции \(\dot{e}_2\). [2, с. 342][3, с. 199]

Если ко вторичной обмотке трансформатора не подключена нагрузка (режим холостого хода), то ЭДС самоиндукции \(\dot{e}_1\) уравновешивает напряжение \(\dot{u}_1\) приложеное к первичной обмотке, что в свою очередь приводит к уменьшению тока \(\dot{\imath}_1\). На выводах вторичной обмотке появляется напряжение \(\dot{u}_2 = \dot{e}_2\), а ток \(\dot{\imath}_2 = 0\). [3, с. 199]

При наличии нагрузки на вторичной обмотке трансформатора (рабочий режим) под действием напряжения \(\dot{u}_2\) по ней начинает протекать ток \(\dot{\imath}_2\). Он в свою очередь создает магнитный поток \(\dot{Ф'}\) который складывается потоком \(\dot{Ф}\).

Трансформатор в цепи постоянного тока

Трансформатор работает только в цепях переменного напряжения и тока. Причина в сущности протекающих в нём процессов - переменный ток протекающий по обмотке создаёт переменный магнитный поток который в свою очередь наводит в другой обмотке переменную ЭДС. Если же подключить трансформатор к цепи постоянного тока, то магнитный поток созданный им будет постоянный \({dФ\over dt} = 0\) и им не будет индуцироваться переменная ЭДС во вторичной и первичной обмотках. В таком режиме ток первичной обмотки достаточно велик, поскольку ограничен только активным сопротивлением, а отсутствие в магнитопроводе магнитного потока \(\dot{Ф'}\) приводит к нагреву стали магнитопровода.

Список использованных источников

1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов - Москва: Высшая школа, 1996. - 623 с.
2. Ломоносов, В.Ю. Электротехника основные понятия: учебное пособие / В.Ю. Ломоносов, К.М. Поливаров - Москва: Государственное энергетическое издательство, 1962. - 392 с.
3. Касаткин А.С. Электротехника: учебное пособие для вузов / А.С. Касаткин, М.В. Немцов - Москва: Энергоатомиздат, 1995. - 240 с.